Forecast double seasonal time series with multiple linear regression in R
I will continue in describing forecast methods, which are suitable to seasonal (or multi-seasonal) time series. In the previous post smart meter data of electricity consumption were introduced and a forecast method using similar day approach was proposed. ARIMA and exponential smoothing (common methods of time series analysis) were used as forecast methods. The biggest disadvantage of this approach was that we created multiple models at once for different days in the week, which is computationally expensive and it can be a little bit unclear. Regression methods are more suitable for multi-seasonal times series. They can handle multiple seasonalities through independent variables (inputs of a model), so just one model is needed. In this post, I will introduce the most basic regression method - multiple linear regression (MLR).
I have prepared a file with four aggregated time series for analysis and forecast. It can be found on my github repo, the name of the file is DT_4_ind. Of course, I’m using EnerNOC smart meter data again and time series were aggregated by four located industries. The file was created easily by the package feather (CRAN link), so only by this package, you can read this file again. The feather is a useful tool to share data for R and Python users.
Data manipulation will be done by data.table package, visualizations by ggplot2, plotly and animation packages.
The first step to do some “magic” is to scan all of the needed packages.
library(feather)
library(data.table)
library(ggplot2)
library(plotly)
library(animation)Read the mentioned smart meter data by read_feather to one data.table.
DT <- as.data.table(read_feather("DT_4_ind"))Let’s plot, what I have prepared for you - aggregated time series of electricity consumption by industry.
ggplot(data = DT, aes(x = date, y = value)) +
geom_line() +
facet_grid(type ~ ., scales = "free_y") +
theme(panel.border = element_blank(),
panel.background = element_blank(),
panel.grid.minor = element_line(colour = "grey90"),
panel.grid.major = element_line(colour = "grey90"),
panel.grid.major.x = element_line(colour = "grey90"),
axis.text = element_text(size = 10),
axis.title = element_text(size = 12, face = "bold"),
strip.text = element_text(size = 9, face = "bold")) +
labs(x = "Date", y = "Load (kW)")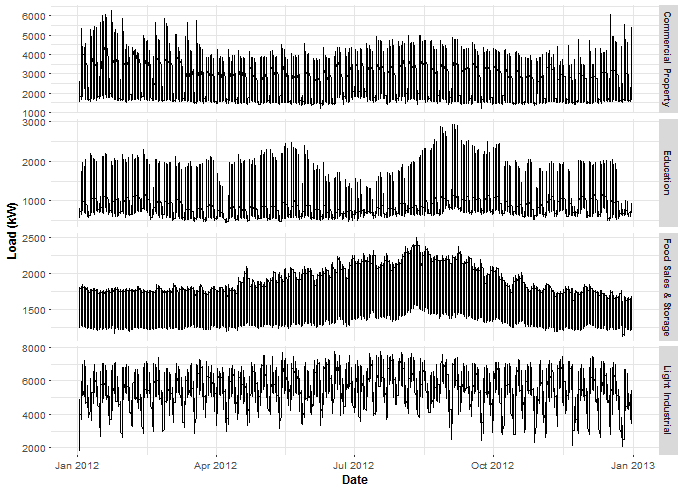
An interesting fact is that the consumption of the industry Food Sales & Storage isn’t changing during holidays as much as others.
Multiple linear regression model for double seasonal time series
First, let’s define formally multiple linear regression model. The aim of the multiple linear regression is to model dependent variable (output) by independent variables (inputs). Another target can be to analyze influence (correlation) of independent variables to the dependent variable. Like in the previous post, we want to forecast consumption one week ahead, so regression model must capture weekly pattern (seasonality). Variables (inputs) will be of two types of seasonal dummy variables - daily (\( d_1, \dots, d_{48} \)) and weekly (\( w_1, \dots, w_6 \)). In the case of the daily variable, there will be \( 1 \), when the consumption during the day will be measured at the particular time, otherwise \( 0 \). In the case of the week variable there will be \( 1 \), when the consumption is measured at the particular day of the week, otherwise \( 0 \).
The regression model can be formally written as:
\[y_i = \beta_1d_{i1} + \beta_2d_{i2} + \dots + \beta_{48}d_{i48} + \beta_{49}w_{i1} + \dots + \beta_{54}w_{i6} + \varepsilon_i,\]where \( y_i \) is the electricity consumption at the time \( i \), where \( i = 1, \dots, N \). \( \beta_1, \dots, \beta_{54} \) are regression coefficients, which we want to estimate. \( d_1, \dots, d_{48} \) and \( w_1, \dots, w_6 \) are dummy independent variables. \( \varepsilon_i \) is a random error. Assumption for the errors are that they are independently identical distributed (i.i.d.) with distribution \( \varepsilon \sim N(0,~\sigma^2) \).
Estimation of regression coefficients is done by ordinary least squares (OLS). So if we wrote our model as:
\[Y = \beta\mathbf{X} + \varepsilon,\]where \( Y \) is a vector of the length \( N \), \( \beta \) is a vector of the length \( p \) and \( \mathbf{X} \) is a matrix of the size \( N\times p,\) then OLS estimation of \( \beta \) is:
\[\hat{\beta} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^TY.\]You are maybe asking, where is independent variable \( w_7 \) or intercept \( \beta_0 \). We must omit them due to collinearity of independent variables. The model matrix \( \mathbf{X} \) must be a regular matrix, not singular. Thereto, intercept has no sense in the time series regression model, because we do not usually consider time 0.
Regression analysis of time series
Let’s finally do some regression analysis of our proposed model. Firstly, prepare DT to work with a regression model. Transform the characters of weekdays to integers.
DT[, week_num := as.integer(as.factor(DT[, week]))]Store informations in variables of the type of industry, date, weekday and period.
n_type <- unique(DT[, type])
n_date <- unique(DT[, date])
n_weekdays <- unique(DT[, week])
period <- 48Let’s look at some data chunk of consumption and do regression analysis on it. I have picked aggregate consumption of education (schools) buildings for two weeks. Store it in variable data_r and plot it.
data_r <- DT[(type == n_type[2] & date %in% n_date[57:70])]
ggplot(data_r, aes(date_time, value)) +
geom_line() +
theme(panel.border = element_blank(),
panel.background = element_blank(),
panel.grid.minor = element_line(colour = "grey90"),
panel.grid.major = element_line(colour = "grey90"),
panel.grid.major.x = element_line(colour = "grey90"),
axis.text = element_text(size = 10),
axis.title = element_text(size = 12, face = "bold")) +
labs(x = "Date", y = "Load (kW)")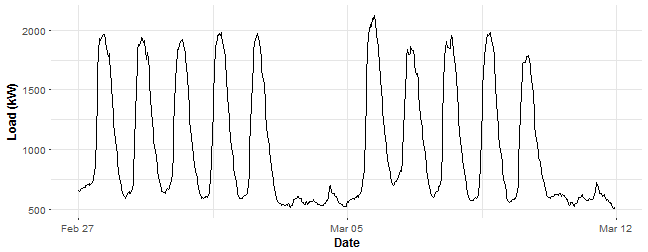
Let’s now create the mentioned independent dummy variables and store all of them in the matrix_train. When we are using the method lm in R, it’s simple to define dummy variables in one vector. Just use as.factor for some vector of classes. We don’t need to create 48 vectors for daily dummy variables and 6 vectors for weekly dummy variables.
N <- nrow(data_r)
window <- N / period # number of days in the train set
# 1, ..., period, 1, ..., period - and so on for the daily season
# using feature "week_num" for the weekly season
matrix_train <- data.table(Load = data_r[, value],
Daily = as.factor(rep(1:period, window)),
Weekly = as.factor(data_r[, week_num]))Let’s create our first multiple linear model with the function lm. lm automatically add to the linear model intercept, so we must define it now 0. Also, we can simply put all the variables to the model just by the dot - ..
lm_m_1 <- lm(Load ~ 0 + ., data = matrix_train)smmr_1 <- summary(lm_m_1)
paste("R-squared: ",
round(smmr_1$r.squared, 3),
", p-value of F test: ",
1-pf(smmr_1$fstatistic[1], smmr_1$fstatistic[2], smmr_1$fstatistic[3]))## [1] "R-squared: 0.955 , p-value of F test: 0"You can see a nice summary of the linear model, stored in the variable lm_m_1, but I will omit them now because of its long length (we have 54 variables). So I’m showing you only the two most important statistics: R-squared and p-value of F-statistic of the goodness of fit. They seem pretty good.
Let’s look at the fitted values.
datas <- rbindlist(list(data_r[, .(value, date_time)],
data.table(value = lm_m_1$fitted.values, data_time = data_r[, date_time])))
datas[, type := rep(c("Real", "Fitted"), each = nrow(data_r))]
ggplot(data = datas, aes(date_time, value, group = type, colour = type)) +
geom_line(size = 0.8) +
theme_bw() +
labs(x = "Time", y = "Load (kW)",
title = "Fit from MLR")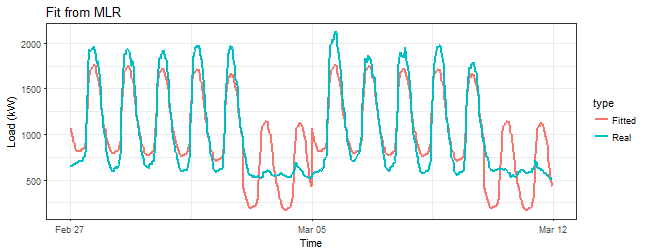
That’s horrible! Do you see that bad fit around 5th March (weekend)? We are missing something here.
Look at the fitted values vs. residuals now.
ggplot(data = data.table(Fitted_values = lm_m_1$fitted.values,
Residuals = lm_m_1$residuals),
aes(Fitted_values, Residuals)) +
geom_point(size = 1.7) +
geom_smooth() +
geom_hline(yintercept = 0, color = "red", size = 1) +
labs(title = "Fitted values vs Residuals")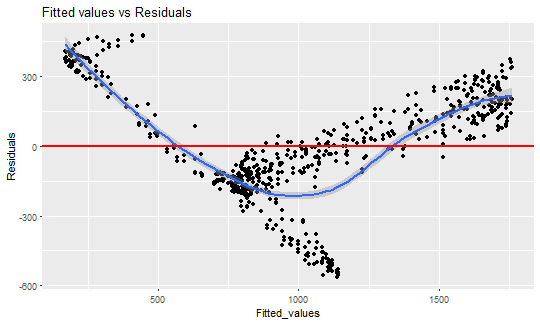
This is the typical example of heteroskedasticity - occurrence of nonconstant residuals (variance) in a regression model. The linear regression has an assumption that residuals must be from \( N(0,~\sigma^2) \) distribution and they are i.i.d. In the other words, the residuals must be symmetrically around zero.
Let’s look at the next proof that our residuals are not normal. We can use normal Q-Q plot here. I’m using the function from this stackoverflow question to plot it by ggplot2.
ggQQ <- function(lm){
# extract standardized residuals from the fit
d <- data.frame(std.resid = rstandard(lm))
# calculate 1Q/4Q line
y <- quantile(d$std.resid[!is.na(d$std.resid)], c(0.25, 0.75))
x <- qnorm(c(0.25, 0.75))
slope <- diff(y)/diff(x)
int <- y[1L] - slope * x[1L]
p <- ggplot(data = d, aes(sample = std.resid)) +
stat_qq(shape = 1, size = 3) + # open circles
labs(title = "Normal Q-Q", # plot title
x = "Theoretical Quantiles", # x-axis label
y = "Standardized Residuals") + # y-axis label
geom_abline(slope = slope, intercept = int, linetype = "dashed",
size = 1, col = "firebrick1") # dashed reference line
return(p)
}ggQQ(lm_m_1)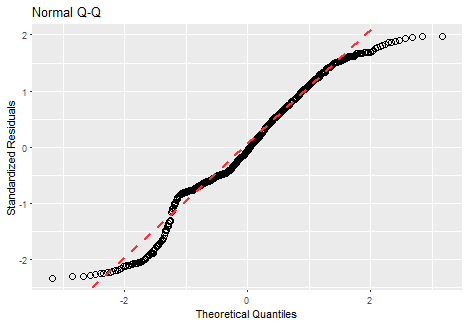
Of course, it is absolutely not normal (points must be close the red line).
What can we do now? Use other regression methods (especially nonlinear ones)? No. Let’s think about why this happened. We have seen on fitted values, that measurements during the day were moved constantly by the estimated coefficient of week variable, but the behavior during the day wasn’t captured. We need to capture this behavior because especially weekends behave absolutely different. It can be handled by defining interactions between day and week dummy variables to the regression model. So we multiply every daily variable with every weekly one. Again, be careful with collinearity and singularity of the model matrix, so we must omit one daily dummy variable (for example \( d_{1} \)). Fortunately, this is done in method lm automatically, when we use factors as variables.
Let’s train a second linear model. Interactions should solve the problem, that we saw in the plot of fitted values.
lm_m_2 <- lm(Load ~ 0 + Daily + Weekly + Daily:Weekly,
data = matrix_train)Look at R-squared of previous model and the new one with interactions:
c(Previous = summary(lm_m_1)$r.squared, New = summary(lm_m_2)$r.squared)## Previous New
## 0.9547247 0.9989725R-squared seems better.
Look at the comparison of residuals of two fitted models. Using the interactive plot plotly here.
ggplot(data.table(Residuals = c(lm_m_1$residuals, lm_m_2$residuals),
Type = c(rep("MLR - simple", nrow(data_r)),
rep("MLR with interactions", nrow(data_r)))),
aes(Type, Residuals, fill = Type)) +
geom_boxplot()
ggplotly()This is much better than the previous model, it seems that interactions are working.
Prove it with a sequence of three plots - fitted values, fit vs. residuals and Q-Q plot.
datas <- rbindlist(list(data_r[, .(value, date_time)],
data.table(value = lm_m_2$fitted.values, data_time = data_r[, date_time])))
datas[, type := rep(c("Real", "Fitted"), each = nrow(data_r))]
ggplot(data = datas, aes(date_time, value, group = type, colour = type)) +
geom_line(size = 0.8) +
theme_bw() +
labs(x = "Time", y = "Load (kW)",
title = "Fit from MLR")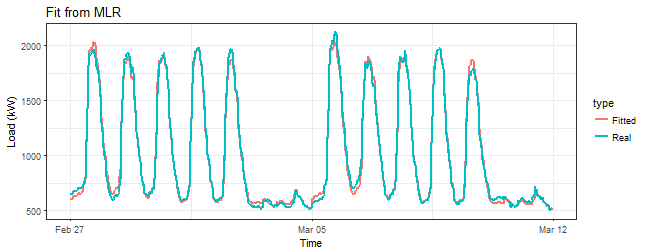
ggplot(data = data.table(Fitted_values = lm_m_2$fitted.values,
Residuals = lm_m_2$residuals),
aes(Fitted_values, Residuals)) +
geom_point(size = 1.7) +
geom_hline(yintercept = 0, color = "red", size = 1) +
labs(title = "Fitted values vs Residuals")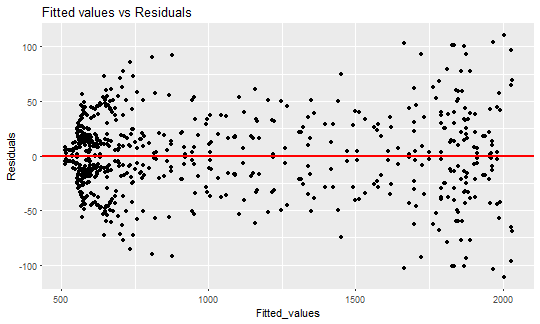
ggQQ(lm_m_2)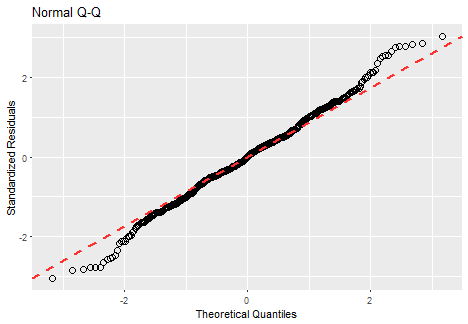
Everything seems much better than in the previous model. The fitted values seem almost perfect.
I also tried to work with a linear trend to boost this model, but it did not help (wasn’t significant). So go ahead and forecast consumption with this model.
Forecast with multiple linear regression
Again, I build function (as in the previous post) to return the forecast of the one week ahead. So we can then simply compare with STL+ARIMA method (was better than STL+ETS). Arguments of this function are just data and set_of_date, so it’s easy to manipulate. Let’s add everything needed to function predWeekReg to create a regression model and forecast.
predWeekReg <- function(data, set_of_date){
# Subsetting the dataset by dates
data_train <- data[date %in% set_of_date]
N <- nrow(data_train)
window <- N / period # number of days in the train set
# 1, ..., period, 1, ..., period - and so on for the daily season
# Using feature "week_num" for the weekly season
matrix_train <- data.table(Load = data_train[, value],
Daily = as.factor(rep(1:period, window)),
Weekly = as.factor(data_train[, week_num]))
# Creation of the model
lm_m <- lm(Load ~ 0 + Daily + Weekly + Daily:Weekly, data = matrix_train)
# Creation of the forecast for one week ahead
pred_week <- predict(lm_m, matrix_train[1:(7*period), -1, with = FALSE])
return(as.vector(pred_week))
}Define MAPE (Mean Absolute Percentage Error) for evaluation of our forecast.
mape <- function(real, pred){
return(100 * mean(abs((real - pred)/real)))
}Now we are ready to produce forecasts. I set training set of the length of two weeks - experimentally proved. In experiments, a whole data set of the length of one year is used, so a forecast for 50 weeks will be produced. A sliding window approach for training is used. Let’s produce (compute) forecast for every type of industry (4), to see differences between them:
n_weeks <- floor(length(n_date)/7) - 2
# Forecasts
lm_pred_weeks_1 <- sapply(0:(n_weeks-1), function(i)
predWeekReg(DT[type == n_type[1]], n_date[((i*7)+1):((i*7)+7*2)]))
lm_pred_weeks_2 <- sapply(0:(n_weeks-1), function(i)
predWeekReg(DT[type == n_type[2]], n_date[((i*7)+1):((i*7)+7*2)]))
lm_pred_weeks_3 <- sapply(0:(n_weeks-1), function(i)
predWeekReg(DT[type == n_type[3]], n_date[((i*7)+1):((i*7)+7*2)]))
lm_pred_weeks_4 <- sapply(0:(n_weeks-1), function(i)
predWeekReg(DT[type == n_type[4]], n_date[((i*7)+1):((i*7)+7*2)]))
# Evaluation (computation of errors)
lm_err_mape_1 <- sapply(0:(n_weeks-1), function(i)
mape(DT[(type == n_type[1] & date %in% n_date[(15+(i*7)):(21+(i*7))]), value],
lm_pred_weeks_1[, i+1]))
lm_err_mape_2 <- sapply(0:(n_weeks-1), function(i)
mape(DT[(type == n_type[2] & date %in% n_date[(15+(i*7)):(21+(i*7))]), value],
lm_pred_weeks_2[, i+1]))
lm_err_mape_3 <- sapply(0:(n_weeks-1), function(i)
mape(DT[(type == n_type[3] & date %in% n_date[(15+(i*7)):(21+(i*7))]), value],
lm_pred_weeks_3[, i+1]))
lm_err_mape_4 <- sapply(0:(n_weeks-1), function(i)
mape(DT[(type == n_type[4] & date %in% n_date[(15+(i*7)):(21+(i*7))]), value],
lm_pred_weeks_4[, i+1]))Similarly, you can do this with the function predWeek from the previous post. I used STL+ARIMA method to compare with the MLR with interactions. Here is the plotly of MAPEs:
For every industry MLR was more accurate than STL+ARIMA, so our basic regression method is working very well for double seasonal time series.
I have created 4 (IMHO) interesting GIFs by the package animation to show whole forecast for a year. I have done it this way for every four industries:
datas <- data.table(value = c(as.vector(lm_pred_weeks_1),
DT[(type == n_type[1]) & (date %in% n_date[-c(1:14,365)]), value]),
date_time = c(rep(DT[-c(1:(14*48), (17473:nrow(DT))), date_time], 2)),
type = c(rep("MLR", nrow(lm_pred_weeks_1)*ncol(lm_pred_weeks_1)),
rep("Real", nrow(lm_pred_weeks_1)*ncol(lm_pred_weeks_1))),
week = c(rep(1:50, each = 336), rep(1:50, each = 336)))
saveGIF({
oopt = ani.options(interval = 0.9, nmax = 50)
for(i in 1:ani.options("nmax")){
print(ggplot(data = datas[week == i], aes(date_time, value, group = type, colour = type)) +
geom_line(size = 0.8) +
scale_y_continuous(limits = c(min(datas[, value]), max(datas[, value]))) +
theme(panel.border = element_blank(), panel.background = element_blank(),
panel.grid.minor = element_line(colour = "grey90"),
panel.grid.major = element_line(colour = "grey90"),
panel.grid.major.x = element_line(colour = "grey90"),
title = element_text(size = 15),
axis.text = element_text(size = 10),
axis.title = element_text(size = 12, face = "bold")) +
labs(x = "Time", y = "Load (kW)",
title = paste("Forecast of MLR (", n_type[1], "); ", "week: ", i, "; MAPE: ",
round(lm_err_mape_1[i], 2), "%", sep = "")))
ani.pause()
}}, movie.name = "industry_1.gif", ani.height = 450, ani.width = 750)Here are the created GIFs:
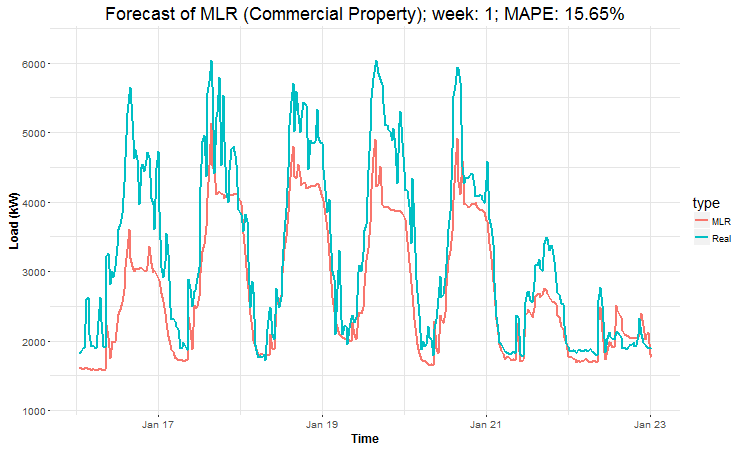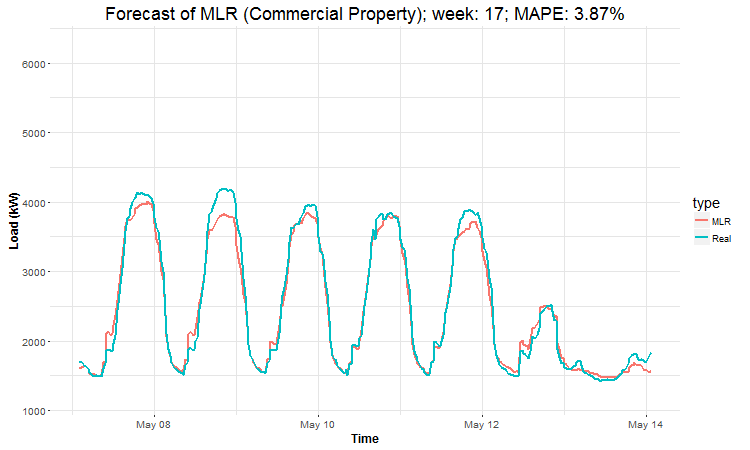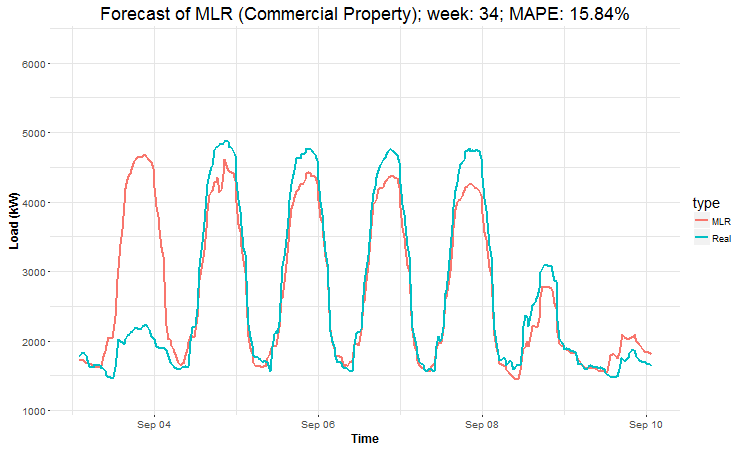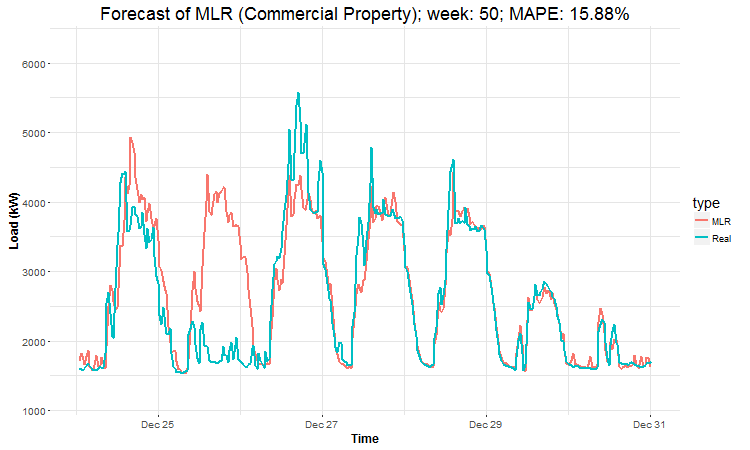
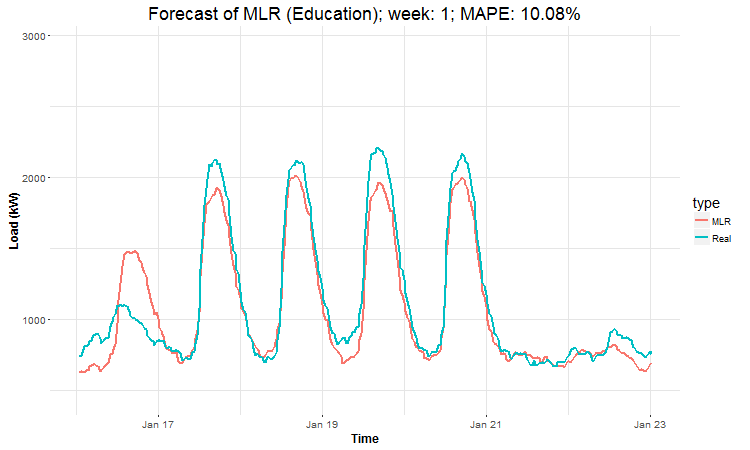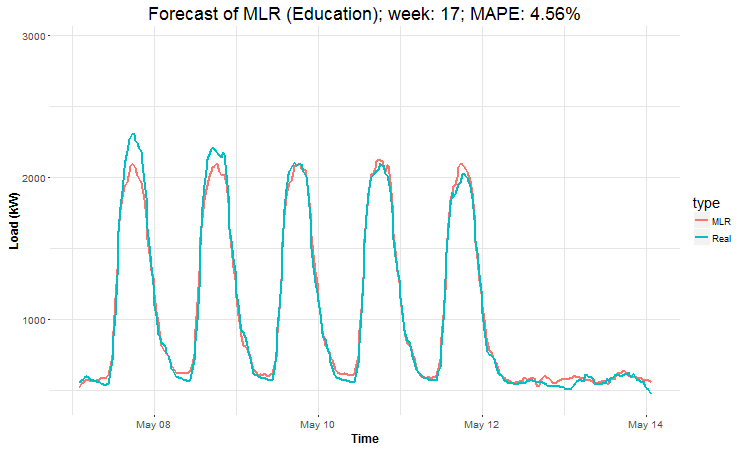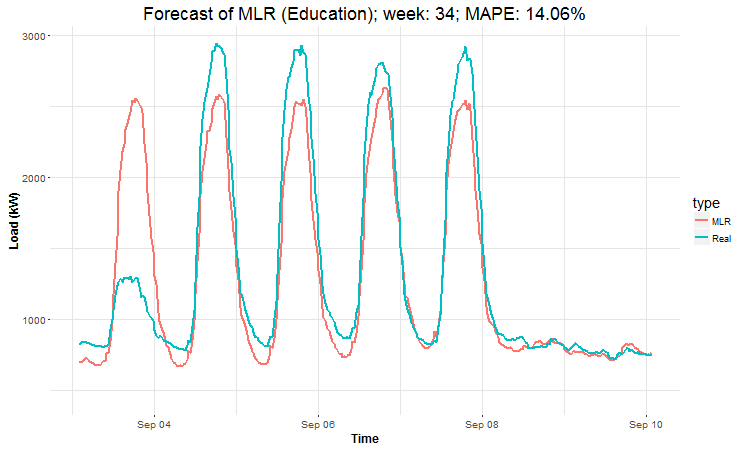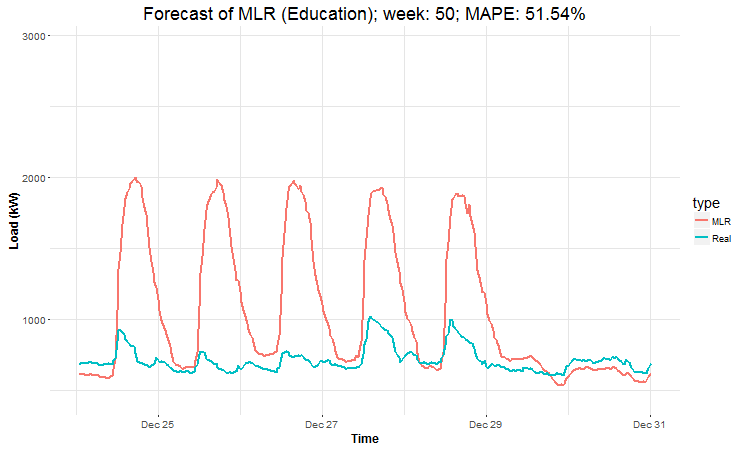
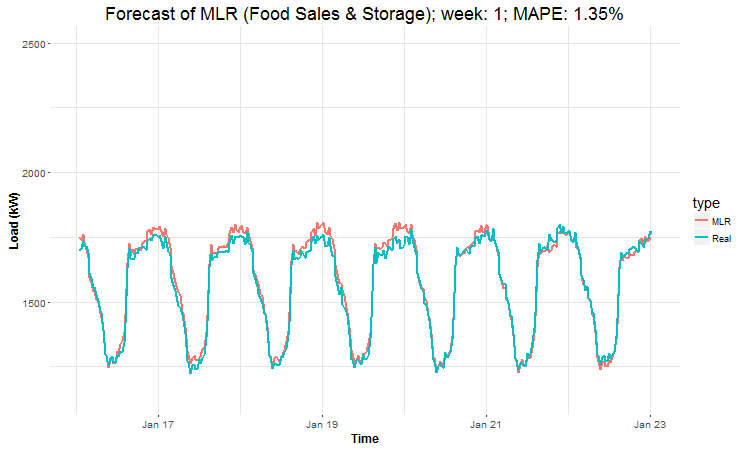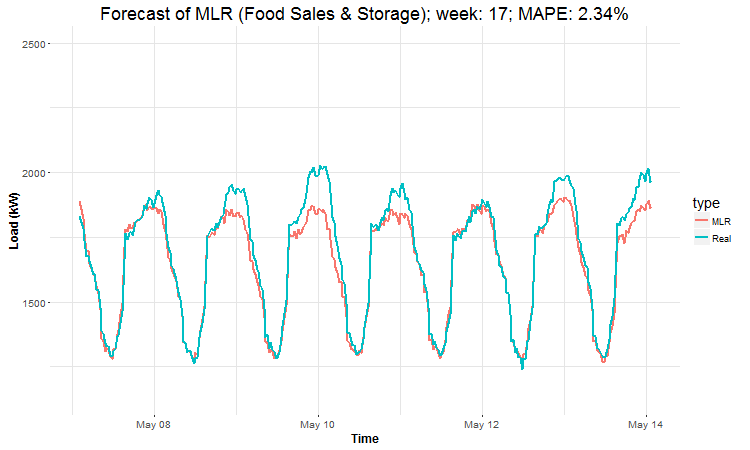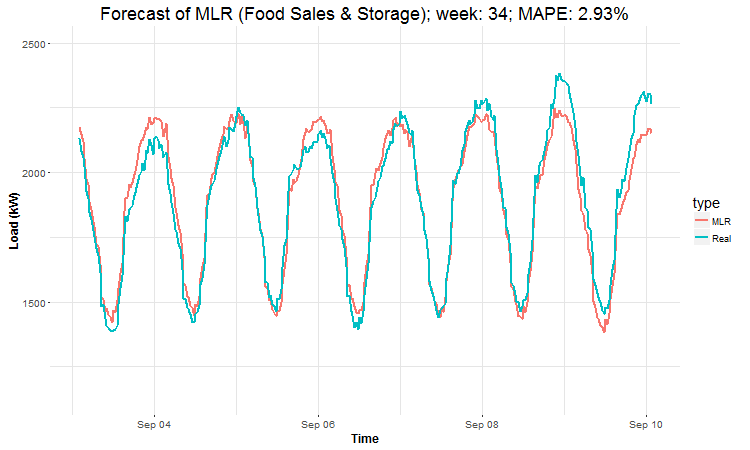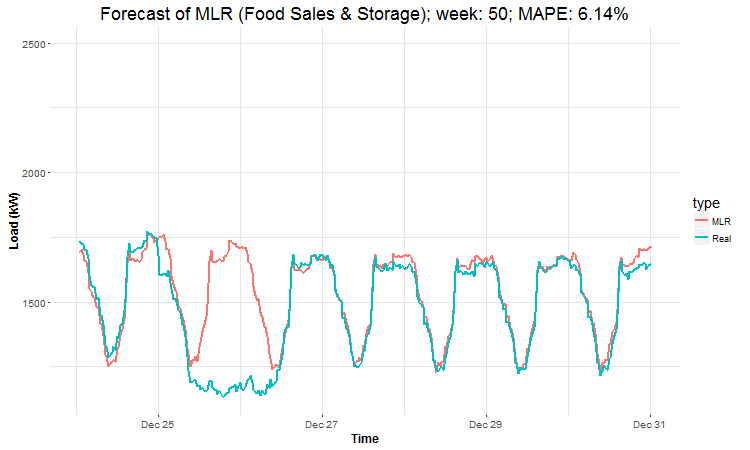
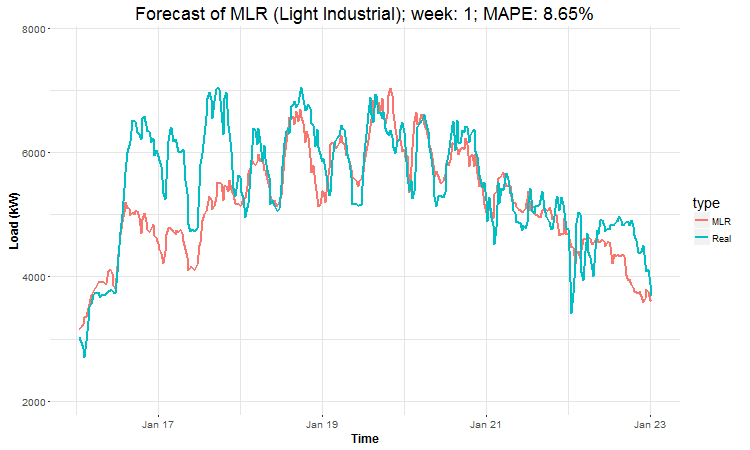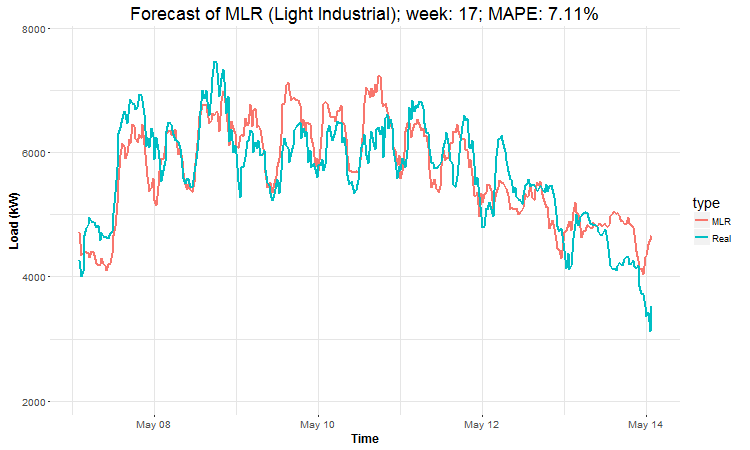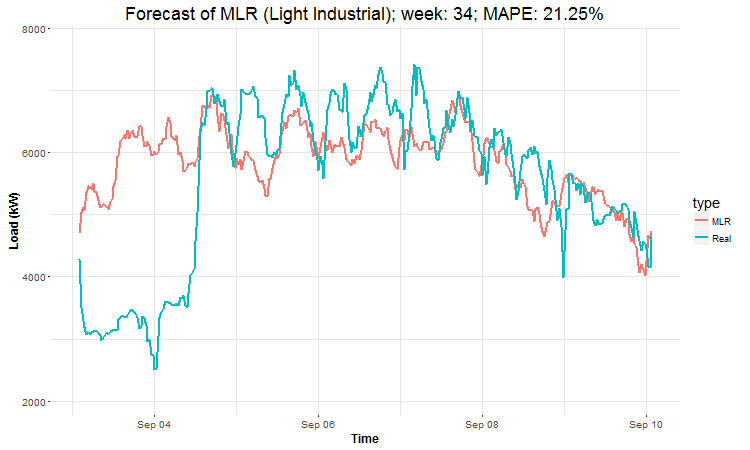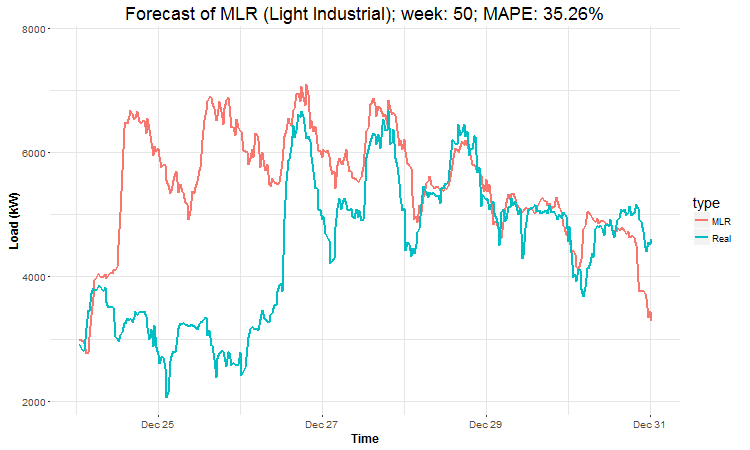
In these animations we can see that the behavior of the electricity consumption can be very stochastic and many external factors influence it (holidays, weather etc.), so it’s a challenging task.
The aim of this post was to introduce most basic regression method, MLR, for forecasting double seasonal time series. By use of the regression analysis, we showed that inclusion of interactions of independent variables to the model can be very effective. This analysis then implies that the forecast accuracy of MLR was much better than with STL+ARIMA method.
In my next post, I will continue with the introduction of regression methods, this time with GAM (Generalized Additive Model).
Script for the creation of this whole post can be found on my github repo.
Seven coffees were consumed while writing this article.
If you’ve found it valuable, please consider supporting my work and...
